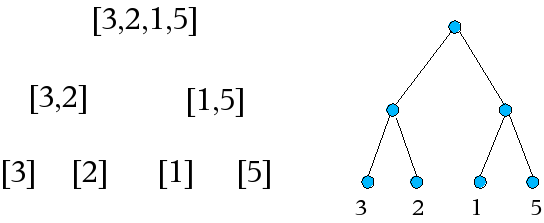
Die Definition in Haskell:
data BTree a = Leaf a
| Fork (BTree a) (BTree a)Bei den beiden Bezeichnern Leaf und Fork handelt es sich um sogenannte Konstruktoren. Sie werden dazu benutzt, Werte dieses Datentyps zu erzeugen. Da die Bäume nicht nur Informationen eines einzelnen Datentyps speichern sollen, wird die in Haskell zur Verfügung stehende Möglichkeit der Typvariablen genutzt. Das kleine 'a' steht für einen beliebigen Datentyp.
Gültige Bäume wären somit:
b1,b2 :: BTree Int b1 = Leaf 10 b2 = Fork (Leaf 11) (Fork (Leaf 6) (Leaf 42))
Einfache binäre Bäume besitzen einige Eigenschaften, von denen zwei im folgenden kurz aufgelistet und beschrieben werden sollen. Diese zu berechnen ist relativ einfach und zeigt, wie Funktionen, die mit Bäumen arbeiten, in Haskell aufgebaut sind.
Größe
Die Größe eines Baumes entspricht der Anzahl der Blattknoten. Eine Funktion, die zu einem Baum diese Eigenschaft berechnet sieht folgendermaßen aus:
size :: BTree a -> Int size (Leaf x) = 1 size (Fork xt yt) = size xt + size yt
Die Signatur besagt, daß die Funktion size einen Parameter des Typs BTree a erhält und einen Wert vom Typ Int zurückliefert. Es wird über die Konstruktoren eine Fallunterscheidung nach Art des als Parameter übergebenen Baums durchgeführt (Pattern Matching). Die erste Funktionsgleichung gilt für einen Blattknoten (Leaf). Das "x" bezeichnet das in diesem Blatt gespeicherte Datum. Die Größe eines Blattes ist konstant eins (1. Gleichung).
Um die Größe von einem Verzweigungsknoten zu berechnen, werden die Größen des linken und des rechten Teilbaums getrennt berechnet und die Resultate anschließend addiert. Für die Verarbeitung der rekursiven Datenstruktur ``Baum'' ist eine rekursive Verarbeitung typisch: Die Blätter entsprechen in diesem Fall dem Basisfall der Rekursion.
Höhe
Als Höhe wird die Entfernung zum weitesten Blatt von der Wurzel aus bezeichnet.
Eine Funktion, die zu einem gegebenen Baum diese Eigenschaft berechnet, sieht wie folgt aus:
height :: BTree a -> Int height (Leaf x) = 0 height (Fork xt yt) = 1 + max (height xt) (height yt)
Die Verarbeitung ähnelt der Berechnungsfunktion für die Baumgröße. Es bietet sich an, wie auch im Kapitel über Listen beschrieben, das Bewegen durch den Baum von der eigentlich problemspezifischen Verarbeitung zu treffen. Dementsprechend wird eine auf den Baum zugeschnittene fold-Funktion verwendet, die folgendermaßen definiert wurde und die Traversierung des Baumes übernehmen soll:
foldBTree :: (a -> b) -> (b -> b -> b) -> BTree a -> b foldBTree f g (Leaf x) = f x foldBTree f g (Fork xt yt) = g (foldBTree f g xt) (foldBTree f g yt)
Der erste Parameter der foldBTree-Funktion ist eine Funktion, die das im Blatt gespeicherte Element verarbeitet. An zweiter Parameterstelle wird eine Funktion zur Verarbeitung der berechneten Werte der Teilbäume erwartet. Sie besitzt zwei Parameter, dies werden die Ergebnisse der verarbeiteten Teilbäume sein. Der letzte Parameter ist der zu verarbeitende Baum.
Die erste Funktionsgleichung zeigt, daß auf den Inhalt eines Blattes einfach die erste Funktion angewendet wird und das Ergebnis zurückgeliefert wird.
Bei inneren Knoten werden zunächst getrennt der linke und rechte Teilbaum verarbeitet und anschließend die Ergebnisse durch die als zweiten Parameter übergebene Funktion verknüpft.
Mit Hilfe dieser Funktion lassen sich nun size und height nachbauen.
size2 = foldBTree (const 1) (+) height2 = foldBTree (const 0) maxsubs where m `maxsubs` n = 1 + m `max` n
Die eingebaute Funktion const bekommt zwei Parameter und liefert als Ergebnis den Wert des ersten Parameters wieder, der zweite wird nicht benutzt. Sie findet hier Verwendung, da für die Bestimmung der Höhe und Größe die Information in den Blättern irrelevant ist.
Man erkennt an der Implementierung von height2, daß die übergebenen Funktionen beliebig kompliziert und wie in diesem Fall auch lokale Funktionen sein können.
Von den zahlreichen Verarbeitungsmöglichkeiten sollen einige grundlegende besprochen werden.
Glätten eines Baumes
Als "Glätten" wird das Umwandeln einer Baumstruktur in eine Liste bezeichnet. Die Reihenfolge der Elemente in der entstehenden Liste entspricht der Abfolge der Elemente im Baum von links nach rechts.
Die Umsetzung in Haskell sieht folgendermaßen aus:
flatten :: BTree a -> [a] flatten (Leaf x) = [x] flatten (Fork xt yt) = flatten xt ++ flatten yt
Der Verarbeitungsablauf entspricht wieder dem bereits bekannten Schema aus dem Kapitel über Eigenschaften.
Der Inhalt eines Blattknotens wird in eine einelementige Liste verpackt, an Verzweigungen werden die Teilbäume getrennt verarbeitet und die Ergebnisse über die Listenverkettung zusammengefasst. Auch hier ließe sich wieder über die fold-Funktion die selbe Funktionalität erreichen.
Erzeugung eines Baumes aus einer Liste
Die zur Glättung inverse Operation ist die Erzeugung von Bäumen aus Listen. Eine übergebene Liste wird in zwei Hälften geteilt; an dieser Stelle im Baum entsteht eine Verzweigung mit den verarbeiteten Teillisten als linken und rechten Teilbaum. Dies wird fortgeführt, bis die Listen nur noch ein Element beinhalten. An dieser Stellen entstehen Blätter mit dem einzigen Element der Liste als Information.

Die Umsetzung in Haskell ist etwas komplizierter als die vorherigen Funktionen:
mkBTree :: [a] -> BTree a
mkBTree xs
| (m == 0) = Leaf (unwrap xs)
| otherwise = Fork (mkBTree ys) (mkBTree zs)
where m = (length xs) `div` 2
(ys, zs) = splitAt m xs
unwrap [x] = xDie Verarbeitung wird hier nicht über Pattern-Matching realisiert, sondern über "Guards". Die lokale Funktion m ermittelt die Länge der halbierten Liste. Beinhaltet sie nur ein Element, wird, wie in der Graphik gezeigt, ein Blatt erzeugt. Die Funktion unwrap liefert das in der Liste gespeicherte Element zurück. Ist die Liste xs länger als ein Element, wird wie beschrieben, eine Verzweigung erzeugt, die Teilbäume werden aus den Listenhälften berechnet.
mapBtree
Ähnlich der map-Funktion bei Listen, ist es häufig sehr hilfreich, solch eine Funktion auch für Bäume zu besitzen. Aus einer Verarbeitungsfunktion für Blattinformationen und einem Baum wird ein neuer Baum berechnet. Die Daten an den Blättern entsprechen dabei den berechneten Funktionswerten der Blattdaten des alten Baumes. Dies entspricht einem der aus der OOP-Welt bekannten Entwurfsmustern, dem Besuchermuster. Die Umsetzung in Haskell ist nahezu selbsterklärend und zeigt die Eleganz der Sprache durch Gleichberechtigung von Funktionen auch als Parametern sehr deutlich.
mapBTree :: (a -> b) -> BTree a -> BTree b mapBTree f (Leaf x) = Leaf (f x) mapBTree f (Fork xt yt) = Fork (mapBTree f xt) (mapBTree f yt)
Bei den bisher dargestellten einfachen binären Bäumen war die Information nur in den Blättern gespeichert. Es gibt allerdings Situationen, in denen die Unterbringung eines weiteren Attributs an den Verzweigungen Algorithmen wesentlich beschleunigen kann. Ein Beispiel soll hier vorgestellt werden.
Haskell bietet auf Listen einen indizierten Zugriff mit Hilfe des (!!)-Operators. Der Zugriff hierauf verläuft allerdings proportional zum Index des gewünschten Elements und ist somit nicht sonderlich effizient.
Eine Erweiterung der Baumstruktur an einer Stelle kann den Zugriff verbessern. Dazu wird an den Verzweigungsknoten ein zusätzliches Attribut aufgenommen, dass die Größe (und damit die Anzahl der Blätter) des linken Teilbaums speichert. Mit Hilfe dieser Information kann nun entschieden werden, ob weiter im linken oder im rechten Teilbaum gesucht werden soll.
Die erweiterte Datendefinition als Codefragment:
data ATree a = Leaf a
| Fork Int (ATree a) (ATree a)Die einzige Änderung ist die zusätzlich Int-Komponente im Fork-Knoten. Es ist allerdings zuzusichern, dass diese stets den richtigen Wert erhält. Dies lässt sich beispielsweise über eine neue Funktion zur Erzeugung kapseln (hier: fork). Im folgenden Beispiel wird diese in der mkATree-Funktion benutzt, um einen semantisch korrekten Baum zu erstellen.
fork :: ATree a -> ATree a -> ATree a fork xt yt = Fork (lsize xt) xt ytlsize :: ATree a -> Int lsize (Leaf x) = 1 lsize (Fork n xt yt) = n + lsize yt
mkATree :: [a] -> ATree a mkATree xs | (m==0) = Leaf (unwrap xs) | otherwise = fork (mkATree ys) (mkATree zs) where m = (length xs) `div` 2 (ys,zs) = splitAt m xs unwrap [x] = x
Die Funktion mkATree entspricht genau der Funktion mkBTree aus dem Kapitel über einfache binäre Bäume. Der einzige Unterschied liegt darin, dass zur Erzeugung von inneren Knoten nicht der Konstruktor des Datentyps benutzt wird sondern der eben beschriebene Wrapper fork. So beschränkt sich die Änderung des Baumerstellungs-Algorithmus auf eine Stelle.
Zuguterletzt soll abschließend die Implementierung des indizierten Zugriffs vorgestellt werden:
retrieve :: ATree a -> Int -> a retrieve (Leaf x) 0 = x retrieve (Fork m xt yt) k = if k < m then retrieve xt k else retrieve yt (k-m)
Wie bereits am Anfang beschrieben, wird an inneren Knoten entschieden, ob das Element mit dem gesuchten Index im linken oder rechten Teilbaum liegt. Bei einer Suche auf der rechten Seite muß jedoch der Index um die Anzahl der Elemente der linken Seite verringert werden. Als Verständnishilfe ein kleines Beispiel: Im linken Teilbaum eines Baumes befinden sich sieben Elemente (dies ist laut Vorgabe auch an der Wurzel als Information gespeichert). Soll nun das neunte Element des Baumes gesucht werden, so ist klar, daß im rechten Teilbaum gesucht werden muß, da im linken ja nur sieben Daten vorhanden sind. Im rechten Baum muß aber nicht nach dem neunten sondern nach dem zweiten Element gesucht werden, die ersten sieben wurden ja "übersprungen".
