Induktion
Übersicht
Strukturelle Induktion
Unter Induktion wird ein logisches Verfahren verstanden, bei dem vom Besonderen auf das Allgemeine geschlossen wird,
z.B. von einer einzelnen Beobachtung auf eine Theorie. In diesem Unterkapitel geht es darum, die Möglichkeiten
von rekursiv definierten Funktionen über einen rekursiven Datentypen zu beurteilen. Dazu bietet sich die Methode
der strukturellen Induktion an. Die Induktion ist auch in vielen anderen Bereichen wie z.B. bei
Listen anwendbar. Dies wird aus den folgenden Vorträgen des Seminars hervorgehen.
Im Falle der natürlichen Zahlen kann das Prinzip der strukturellen Induktion wie folgt erklärt werden:
Um zu zeigen, dass eine Eigenschaft P(n) für jede endliche Zahl n aus Nat gilt, ist es
ausreichend zu zeigen, dass:
- Fall 1 (Zero): P(Zero) gilt und
- Fall 2 (Succ n) wenn P(n) gilt, dass in dem Fall auch P(Succ n) gültig ist.
Die Induktion ist aus dem gleichen Grund gültig, aus dem rekursive Definitionen gültig sind: Jede endliche
Zahl ist entweder
Zero oder entspricht der Form
Succ n, wenn
n eine endliche Zahl ist. Durch die Prüfung
des ersten Falls wird nachgewiesen, dass
P(Zero) gültig ist. Die Prüfung des zweiten
Falls ergibt, dass die Funktion
Succ Zero wahr ist, wenn sie bereits für
Zero wahr ist.
Mit dem selben Argument ist sie gültig für
Succ(Succ Zero) usw.
Dieses Prinzip der Induktion muss ausgeweitet werden, um sicherzustellen, dass alle Ausdrücke gültig sind.
Die Erweiterung wird aber auf den nächsten Abschnitt
(s. vollständige Induktion)
verschoben.
Als Beispiel wird geprüft, ob Zero + n = n für alle endlichen Zahlen gültig ist. Das bedeutet, dass
Zero links-assoziativ bzgl. (+) ist.
Zur Erinnerung ist (+) definiert durch die zwei Gleichungen (die Nummerierung dient der Orientierung):
(1.) m + Zero = m
(2.) m + Succ n = Succ(m + n)
|
Beweis: Dieser wird geführt durch Induktion auf n. Präziser wird jetzt für P(n) die
Induktionshypothese Zero + n = n benutzt. Zur Einführung sind die betreffenden Stellen im Code
unterstrichen, was aber in den nächsten Beispielen ausdrücklich unterlassen wird.
Fall 1 (Zero): Es muss gezeigt werden, dass Zero + Zero = Zero gilt. Dies ergibt sich aber schnell
aus der 1. Gleichung für (+).
Fall 2 (Succ n): Hier muss gezeigt werden, dass Zero + Succ n = Succ n ergibt. Dies wird erreicht
durch die Vereinfachung des linken Ausdrucks:
Zero + Succ n
= {2. Gleichung für (+)}
Succ(Zero + n)
= {Induktionshypothese}
Succ n
|
Dieses Beispiel zeigt das Vorgehen, das für den induktiven Beweis genutzt wird. Dabei wird jeder
Fall einzeln behandelt.
Als zweites und etwas komplizierteres Beispiel wird ein bekanntes mathematisches Gesetz angeführt, das für
alle endlichen natürlichen Zahlen x, m und n gilt:
Für den Beweis werden, neben der oben schon wiederholten Definition für (+), auch die Definitionen für
(*) und (^) aus dem vorherigen Kapitel benötigt. Sie lauteten:
(1.) m * Zero = Zero
(2.) m * Succ n = (m * n) + m
(1.) m ^ Zero = Succ Zero
(2.) m ^ Succ n = (m^n) * m
|
Beweis: Die Prüfung wird durch Induktion auf n durchgeführt. Als Induktionshypothese dient
die obige Gleichung:
Es ist wichtig, die Variable zu nennen, auf die die Induktion durchgeführt wird. In diesem Fall gibt es die
drei Möglichkeiten x, m und n.
Fall 1 (Zero): Die Idee ist, in der Hypothese n durch Zero zu substituieren und dann
beide Seiten unabhängig zu vereinfachen.
Wird diese schrittweise Substitution durchgeführt, ergibt sich für die linke Seite der Gleichung:
x^(m + Zero)
= {1. Gleichung für (+)}
x^m
|
Für die rechte Seite ergibt sich:
(x^m) * (x^Zero)
= {1. Gleichung für (^) bzgl. (x^Zero)}
(x^m) * Succ Zero
= {2. Gleichung für (*)}
(x^m) * Zero + (x^m)
= {1. Gleichung für (*) bzgl. (x^m) * Zero}
Zero + (x^m)
= {Im ersten Beispiel nachgewiesene Induktionshypothese}
x^m
|
Beide Seiten ergeben das selbe vereinfachte Ergebnis, also sind sie gleich. Die Vereinfachung des rechten Ausdrucks
ist die kompliziertere der beiden, da sie den Beweis enthält, dass Succ Zero rechts-assoziativ
bzgl. der Multiplikation ist.
Fall 2 (Succ n): Die Idee dabei ist ebenfalls, in der Hypothese n durch Succ n zu substituieren
und dann beide Seiten unabhängig zu vereinfachen.
Durch die Substitution ergibt sich für die linke Seite der Gleichung:
x^(m + Succ n)
= {2. Gleichung für (+)}
x^Succ(m + n)
= {2. Gleichung für (^)}
(x^(m + n)) * x
= {Induktionshypothese}
((x^m) * (x^n)) * x
|
Für die rechte Seite ergibt sich nun:
(x^m) * (x^Succ n)
= {2. Gleichung für (^) bzgl. (x^Succ n)}
(x^m) * ((x^n) * x)
|
Die beiden Vereinfachungsergebnisse unterscheiden sich voneinander. Sie sind aber gleich unter der Annahme, dass (*) assoziativ
ist. Der Beweis dieser Tatsache wird aus Gründen der Übersichtlichkeit unterlassen.
Die Prüfung erfolgt immer durch eine fast automatische Schrittfolge:
- Auf beiden Seiten substituieren und jeweils vereinfachen.
- Dabei wird jeder Vereinfachungsschritt eindeutig durch die Form des aktuellen Ausdrucks bestimmt.
Der einzig entscheidende Prozess bei der Induktion ist die Wahl der richtigen Variablen. In diesem Beispiel existieren
drei Variablen, aber nur zwei davon führen zum gewünschten Ziel (m und n).
Die Induktion auf n wurde im obigen Beispiel schon behandelt. Im nachfolgenden Beispiel wird nun der (etwas kompliziertere) Beweis dargestellt,
wenn die Entscheidung auf m fällt:
Beweis: Diesmal durch Induktion auf m.
Fall 1 (Zero): Es ergibt sich für die linke Seite der Gleichung:
x^(Zero + n)
= {Forderung 1: Zero + n = n für alle n}
x^n
|
Für die rechte Seite ergibt sich:
(x^Zero) * (x^n)
= {1. Gleichung für (^)}
Succ Zero * (x^n)
= {Forderung 2: Succ Zero * n = n für alle n}
x^n
|
Die beiden Forderungen sind, dass Zero links-assoziativ bzgl. (+) ist und das Succ Zero links-assoziativ
bzgl. (*) ist. Ein Beweis dieser beiden Forderungen wird aber an dieser Stelle unterlassen.
Fall 2 (Succ m): Es ergibt sich für die linke Seite der Gleichung:
x^(Succ m + n)
= {Forderung 1: Succ m + n = Succ(m + n)}
x^Succ(m + n)
= {2. Gleichung für (^)}
(x^(m + n)) * x
= {Induktionshypothese}
((x^m) * (x^n)) * x
|
Für die rechte Seite ergibt sich:
(x^Succ m) * (x^n)
= {2. Gleichung für (^)}
((x^m) * x) * (x^n)
|
Nun ist erkennbar, dass eine zweite Annahme benötigt wird, um festzustellen, das beide Seiten gleich sind.
Es muss bewiesen werden, dass (*) kommutativ sowie assoziativ, also x * y = y * x ist.
Die Induktion auf m ist komplizierter als die erste auf n, da sie vier Annahmen enthält. Diese
Annahmen müssen, jede für sich, wiederum durch Induktion bewiesen werden.
Ziel dieses Abschnitts war es zu verdeutlichen, dass die Wahl der Variablen entscheidend für den weiteren
Verlauf der Substitution ist. In diesem Fall ist es vernünftig, mit der Induktion auf n zu beginnen, da (+)
durch Rekursion auf seinem zweiten Argument definiert ist. Dadurch ist der erste Schritt des Beweises auf der linken
Seite einfach und ebenso wird der Rest des Beweises einfacher.
[nach oben]
Vollständige Induktion
Nachdem im letzten Abschnitt auf die Induktion in vereinfachter Form eingegangen wurde, soll in diesem Abschnitt die
vollständige Induktion behandelt werden. Das bedeutet, dass es nicht nur die Prinzipien der Induktion von
endlichen Zahlen aus Nat gibt, sondern es soll ebenso dargestellt werden, dass dies auch für jede
partielle Zahl möglich ist.
Um die Induktion zu vervollständigen, müssen allerdings drei
Beweise angetreten werden:
- Fall 1: (
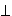 ) Dass P(
) Dass P(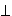 ) gilt,
) gilt,
- Fall 2: (Zero) P(Zero) gilt und
- Fall 3: (Succ n) wenn P(n) gilt, dass in dem Fall auch P(Succ n) gültig ist.
Die im letzten Abschnitt vorgestellte Induktion wird also um den Fall der undefinierten Zahlen ergänzt.
Es könnte der zweite Fall ausgelassen werden, aber dann kann nur festgestellt werden, dass
P(n) für
jede partielle Zahl gilt. Der Grund für die Gültigkeit des Prinzips ist, dass jede partielle Zahl entweder
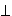
oder der Form
Succ n für einige Zahlen
n entspricht.
Diese "Zero-Problematik" wird im Folgenden am Beispiel von m + n = n für alle Zahlen m und alle partiellen Zahlen n gezeigt.
Beweis: Dieser wird durch Induktion einer partiellen Zahl auf n durchgeführt.
Fall 1 (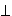 ):
): Die Gleichung
m + 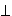 =
= 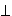
folgt in einem
Schritt durch "case exhaustion" in der Definition von (+). Das bedeutet, dass
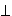
weder auf die Muster von
Zero noch
auf die von
Succ n zutrifft.
Fall 3 (Succ n): Für die linke Seite ergibt sich:
m + Succ n
= {2. Gleichung für (+)}
Succ(m + n)
= {Induktionshypothese}
Succ n
|
Ist die rechte Seite ebenfalls Succ n, so ist es bewiesen.
Der ausgelassene zweite Fall m + Zero = Zero ist falsch, was bedeutet, dass die Gleichung m + n = n für endliche Zahlen nicht gilt.
Durch dieses Vorgehen ist es einfach, Induktion auf partielle Zahlen anzuwenden. Ebenso ist es möglich zu zeigen,
dass eine Gleichung für unendliche Zahlen gilt, wenn sie für partielle Zahlen gilt. Dies soll hier aber
nicht weiter vertieft werden. Im Folgenden wird einfach angenommen, dass m + infinity = infinity für alle
Zahlen m gilt.
[nach oben]
Programmsynthese
In den vorangegangenen Beweisen wurden Funktionen definiert und durch Induktion bestimmte Eigenschaften nachgewiesen.
Anders herum ist es aber auch möglich, die Induktion zu nutzen, um Definitionen von Funktionen zu synthetisieren.
Mit anderen Worten, die Programme so zu erstellen, dass sie den gewünschten Eigenschaften entsprechen.
Die Programmsynthese soll durch ein einfaches Beispiel dargestellt werden. Angenommen die Subtraktion von
natürlichen Zahlen wird durch folgende Gleichung spezifiziert:
(m + n) - n = m für alle n und m
|
Diese Spezifikation stellt keine sehr konstruktive Definition von (-) dar, sondern enthält lediglich eine
zu erfüllende Eigenschaft. Trotzdem kann die gegebene Gleichung benutzt werden, um aus ihr mittels Induktion
eine passende Definition für (-) zu synthetisieren.
Im Gegensatz zu vorhergehenden Beweisen, wird jetzt die Gleichung als Ganzes hergenommen. Grund: Eine unabhängige
Vereinfachung auf beiden Seiten ist wegen noch fehlender Regeln nicht möglich.
Fall 1 (Zero): Vereinfachung, indem n durch Zero substituiert wird:
(m + Zero) - Zero = m
≡ {1. Gleichung für (+)}
m - Zero = m
|
Hieraus wird m - Zero = m genutzt, um diesen Fall zu erfüllen. Das Symbol '≡' dient dazu, Berechnungsschritte abzugrenzen,
da hier nicht mehr mit Werten von Datentypen, sondern mit mathematischen Behauptungen umgegangen wird.
Fall 2 (Succ n): Es wird vereinfacht, indem n durch Succ n substituiert wird:
(m + Succ n) - Succ n = m
≡ {2. Gleichung für (+)}
Succ(m + n) - Succ n = m
≡ {Hypothese (m + n) - n = m}
Succ(m + n) - Succ n = (m + n) - n
|
Wird m + n in der letzten Gleichung durch m ersetzt, so kann Succ m - Succ n = m - n benutzt werden,
um die Vorgaben zu erfüllen. Durch diese Vereinfachungen wurde nun Folgendes abgeleitet:
m - Zero = m
Succ m - Succ n = m - n
|
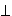 ) Dass P(
) Dass P(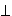 ) gilt,
) gilt,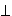 ) Dass P(
) Dass P(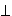 ) gilt,
) gilt,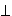 oder der Form Succ n für einige Zahlen n entspricht.
oder der Form Succ n für einige Zahlen n entspricht.
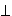 ): Die Gleichung m +
): Die Gleichung m + 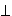 =
= 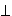 folgt in einem
Schritt durch "case exhaustion" in der Definition von (+). Das bedeutet, dass
folgt in einem
Schritt durch "case exhaustion" in der Definition von (+). Das bedeutet, dass 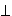 weder auf die Muster von Zero noch
auf die von Succ n zutrifft.
weder auf die Muster von Zero noch
auf die von Succ n zutrifft.